Introducing Point-in-Time Data: Addressing the Mutability of On-chain Metrics
We discuss when and how quickly on-chain metrics at Glassnode get updated and analyze the impact and magnitude of data updates. Further, we introduce a broad set of point-in-time metrics that do not suffer from look-ahead bias, making them the ideal candidates for applications in backtesting.
At Glassnode we provide you with the most comprehensive suite of on-chain metrics across various crypto assets. As by its name, such on-chain data is directly derived from the actual activity and behavior on the blockchain. Transforming the raw on-chain data into metrics is not always a straightforward process and comes with challenges and caveats, with several aspects being of high significance to users of the metrics. In this article, we aim to shine more light on the underlying processes in our metric computations and the nature of on-chain data in general.
In particular, we want to address the following questions:
- Data availability: How exactly does the data contained in the blockchain propagate into our metrics and how long does this take? When can a data point be considered “complete”?
- Data mutability: To which extent can on-chain metrics change as time progresses? What are reasons for that, what are the related timescales and what is the expected magnitude of possible data updates?
As we will see below, the possibility of changing data values renders the use of such metrics problematic for some applications, notably for backtesting. Therefore we release a new set of metrics that are tailored towards such use cases, where immutable historic data is of uttermost importance: point-in-time metrics.

Data Availability
Both on a data level and in a literal sense, the constituents of a blockchain are simply “blocks”. Below we follow a block’s path through various stages: from its creation and distribution in the global network into our own infrastructure and finally into our metrics. In order to understand when a new data point becomes available in our metrics, it is crucial to understand these individual steps, and how each of them can have an effect on the time it takes for our metrics to update.
A block’s journey into our metrics
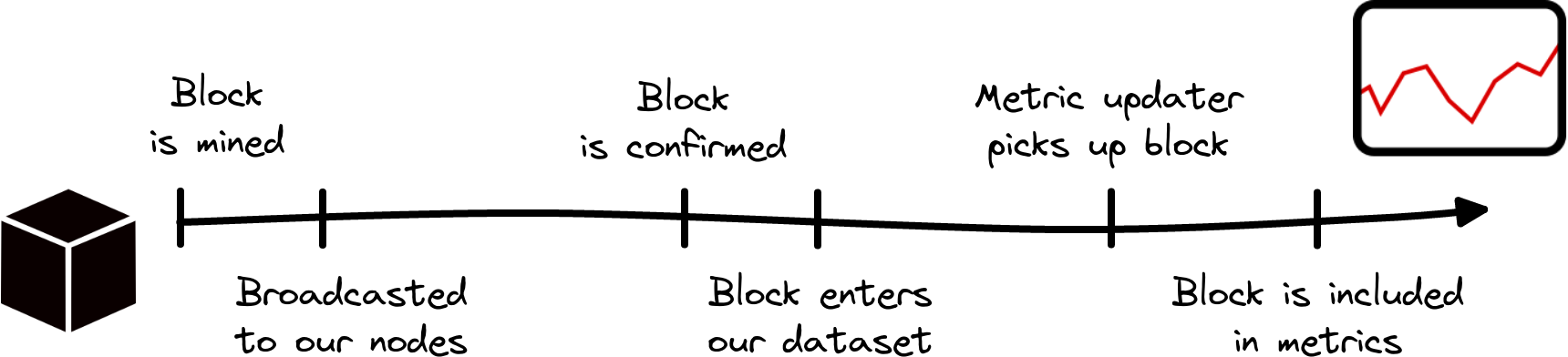
Step 1: A block is mined
New blocks are appended to a chain one at a time, by always referencing the preceding blocks. For Bitcoin this is achieved via a Proof-of-Work (PoW) scheme. In simple terms this means: Once miners solve a cryptographic challenge, their generated blocks become a valid extension to the chain and can be distributed across a network of nodes. These in turn validate the blocks and eventually consensus reached by agreeing that the longest chain represents the new state of the blockchain. In contrast, Ethereum recently switched to Proof-of-Stake (PoS). In this consensus mechanism the role of miners is taken by validators, who must deposit a stake of 32 ETH to participate. Without going into any details here, we note that validators are algorithmically assigned as block producers and the blocks are subsequently attested by the rest.
Block timestamps
But let us go back one step: Apart from the cryptographic solution (PoW) or the consensus info (PoS), a block contains a number of transactions (that e.g. in case of Ethereum may reflect complex smart contract calls) and, amongst other data, a fixed timestamp that is associated with the block’s creation time. It is this timestamp that will later define which time period of the metric the block will contribute to.
In PoW blockchains the interval between two adjacent blocks is probabilistic, with only the average duration indirectly controlled via the Difficulty. For BTC and ETH (“pre-Merge”) we show the distribution of these intervals in Fig. 2, with the interval on the x-axis and the frequency on the y-axis. In “post-Merge” ETH with its PoS mechanism blocks are created in fixed slot intervals, forming a discrete distribution.
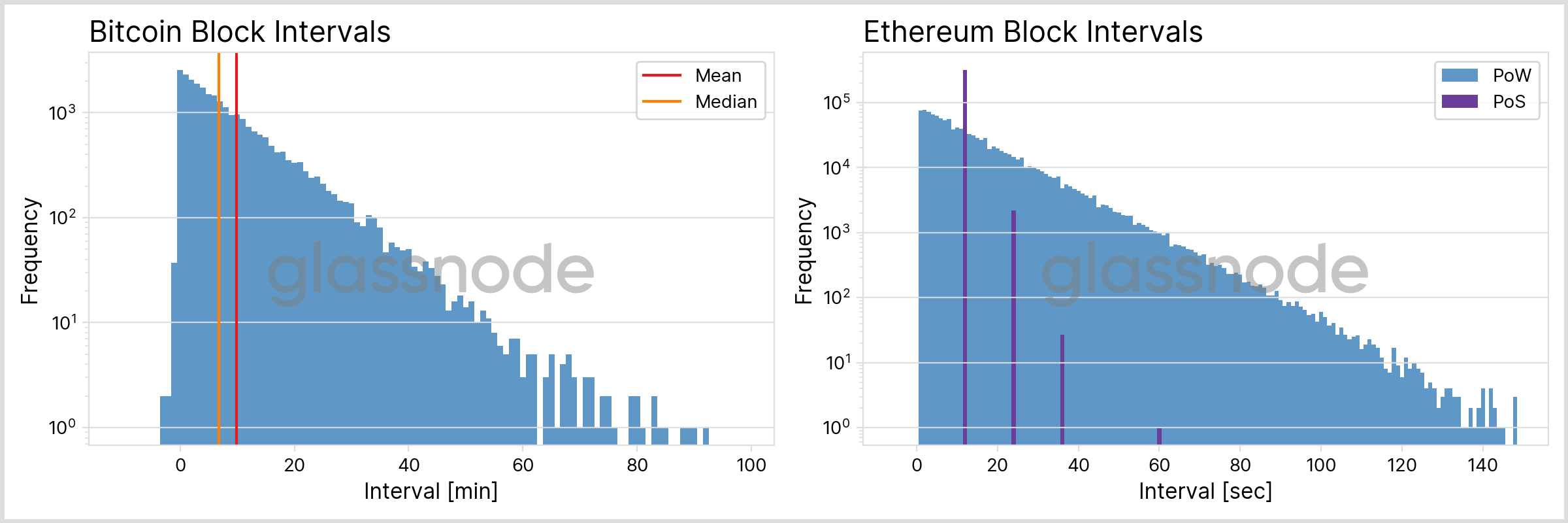
| BTC | ETH (PoW) | ETH (PoS) | |
|---|---|---|---|
| mean | 9:50 min | 13 s | 12 s |
| median | 6:47 min | 10 s | 12 s |
| 90th percentile | 22:38 min | 31 s | 12 s |
| 99th percentile | 44:44 min | 1:01 min | 12 s |
| max | 1:45 h | 2:52 min | 1:00 min |
From the graphs we can conclude the following:
- While the majority of block intervals is small, in some cases the time between blocks can be a multiple of the average interval: For BTC we observe numbers above 1 hour (whereas the mean interval is around 10 minutes only), for ETH (PoW) it might take more than 2 minutes for a new block to be appended to the chain in the worst case (see the table above for more detailed numbers).
- The shape of the continuous curves is indicative of an Exponential Distribution. We will elaborate on this aspect in more detail below.
- For ETH (PoS) the block interval is concentrated at 12 seconds, which is the slot time interval enforced by the consensus mechanism. Multiples of this fundamental time scale indicate a “missed block”, i.e. situations in which a validator did not propose a new block in time.
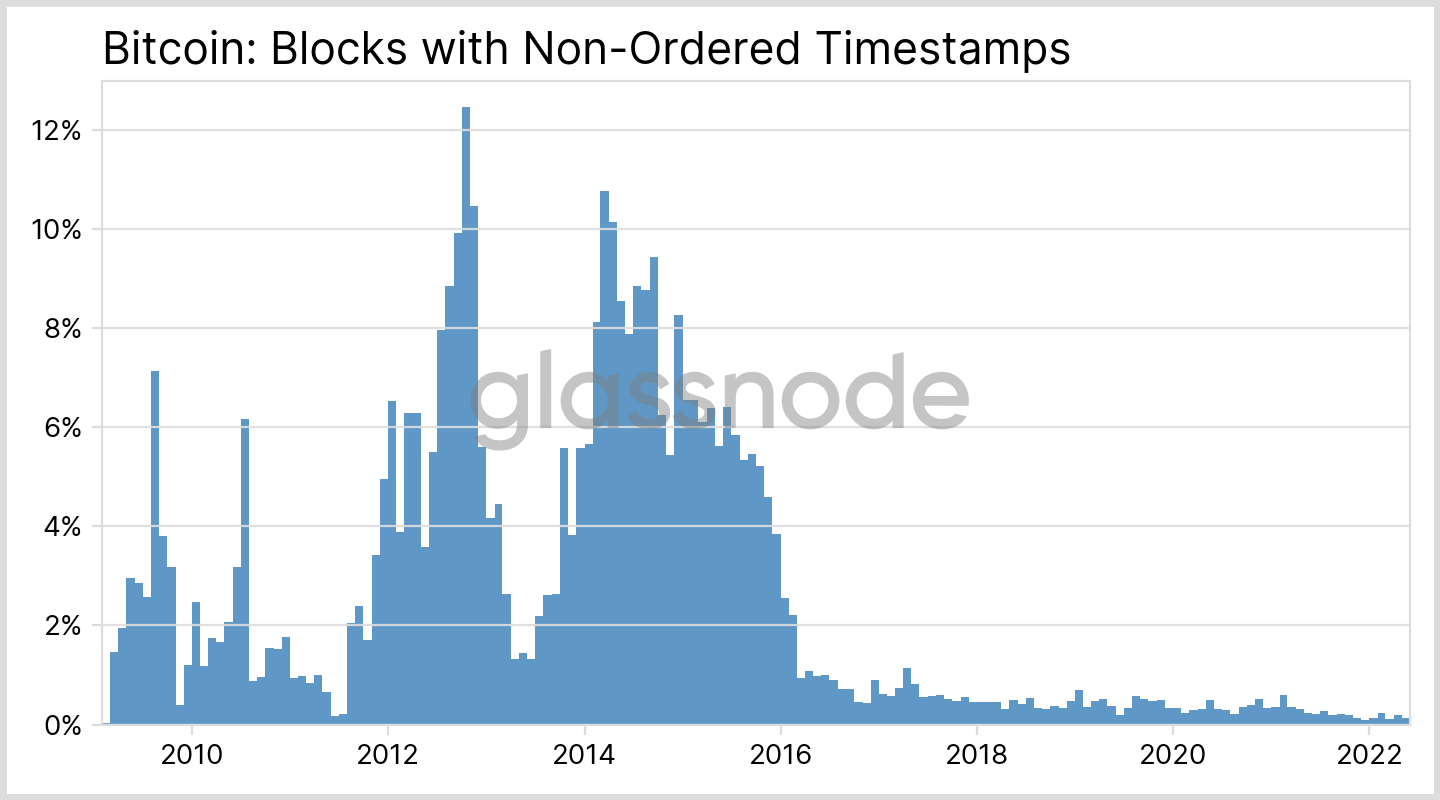
Counterintuitively, we also observe some negative time intervals for BTC: Usually we can assume that the clocks used by the different miners are synced, thanks to standards like the Network Time Protocol. This means that the timestamps of subsequent blocks are in order and always increasing. In fact, this is a strict requirement for Ethereum, as defined in its Yellow Paper. For Bitcoin, though, the conditions are more relaxed and no monotonic timestamp sequences are enforced. In the last few years, though, out-of-order timestamps became scarce (see Fig. 3).
Step 2: Broadcast
After a new BTC block is created (“mined”), it is broadcasted across the global network of nodes. This happens on a timescale much faster than the mean block interval. For example, in the case of BTC it takes only a few seconds until most of all network peers receive a new block, whereas the interval between two blocks is around 10 minutes on average. This propagation delay applies to general nodes, but in fact the data transfer between miners can be even faster due to techniques like FIBRE. We can very well assume that the different mining pools try to reduce latency as much as possible, to minimize blockchain forks and to make mining more cost efficient.
Similar, the distribution of new blocks in ETH (PoS) is tied to their validation and hence happens on a very fast time scale as well.
Step 3: Block confirmation
Now let us see what happens with the block in the Glassnode infrastructure: Before we make use of the data contained in a new block that reaches our own nodes, we wait until the block is confirmed. The reason to wait for block confirmations is to reduce the amount of data changes, e.g. by reducing the probability of initial inclusion of orphan blocks. For BTC and ETH, for example, we wait for 1 and 12 additional blocks, respectively, until a block really enters our datasets.
Side note: The total delay imposed by this safety measure can be described mathematically. For ETH (PoS), where the time between subsequent blocks is almost always 12 seconds, this takes less than 2.5 minutes (12 × 12 seconds). For Bitcoin, assuming synchronized clocks of the miners and a rather constant hash rate, we can model the mining of new blocks as a Poisson process. In fact, this is substantiated by the exponential distributions which we observed in Fig. 2. Therefore the time between a certain number of blocks follows an Erlang distribution, where the number of confirming blocks determines the “shape” and the mean block interval the “rate” parameter. Adding a constant offset to take into account the propagation delay and the time it takes to write the data to our datasets, this approach very well matches the actual total delay, as discussed so far.
Step 4: Metric updates
It is now time for the last step of the block’s journey towards its inclusion in a metric: One of our programs analyzes the updated dataset, performs some computations and appends new data points to our metric. These updaters are currently scheduled to run in intervals that depend on the metric resolution. For example, our updaters run at 00:00:00 UTC for our metrics with 1 day resolution, and every full ten minutes for 10 minute resolution metrics (for details see our documentation here). Thus, even for the latter, we have to wait an additional zero to ten minutes, on average five minutes, until the block’s data gets picked up. The actual runtime of the updater strongly depends on the metric complexity and can be between a few seconds up to several minutes, with examples given in Fig. 4 below.
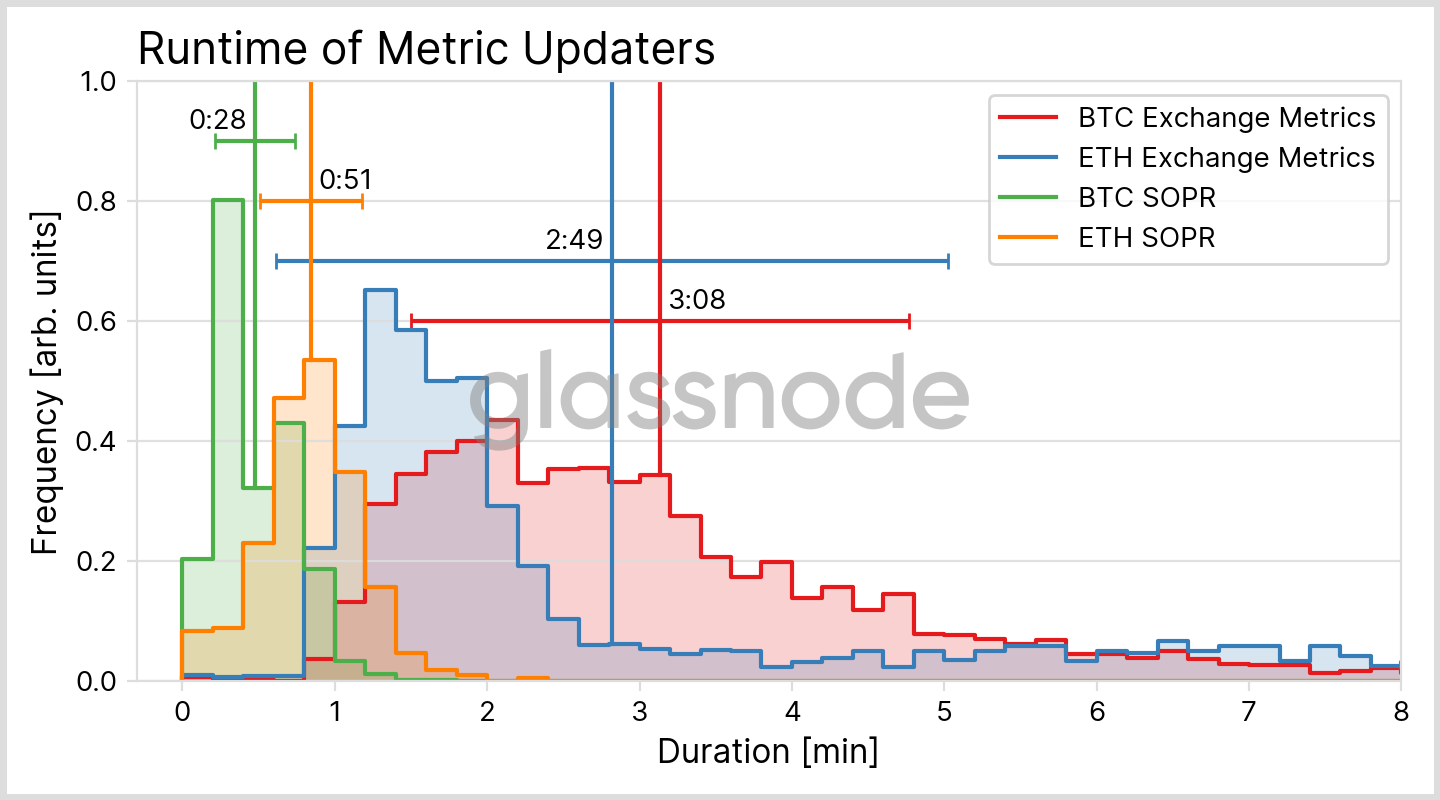
The journey in summary
Let us summarize the different contributions that make up the total time until our metrics get updated:
- After a block has been successfully created, it is propagated across the different nodes in the network, with the whole process taking a few seconds.
- Before we move the block into our datasets, we wait for confirmation via a number of subsequent blocks depending on the asset. Depending on the blockchain and its mean block interval, the required time is in the range of a few 1–10 minutes. In extreme cases, confirmation can take one hour or longer.
- Writing to our datasets is usually finished in less than a minute.
- The metric computation starts with a delay between zero and ten minutes (for metrics with a resolution of 10 minutes).
- It takes the updaters a few seconds up to a few minutes to produce the new data point and make it available via our API.
Since the different contributions listed above are independent, the combined delay can be computed in form of a convolution of their individual distributions.
Numbers, please
To gauge if our understanding as described above is comprehensive, let us look at some real-world data. To this end, we chose the number of Addresses Depositing to Exchanges as a representative metric for both BTC and ETH, evaluated our log files and extracted all required timestamps.
The result of this analysis is depicted in Fig. 5 below. The theoretically expected distribution was derived by fitting one free parameter only, which is a shift along the time axis, taking into account block propagation from the miner to our nodes and the combined runtime of our software. Note that the shape of the distribution is unaffected by this free parameter and exclusively determined by the model described above.
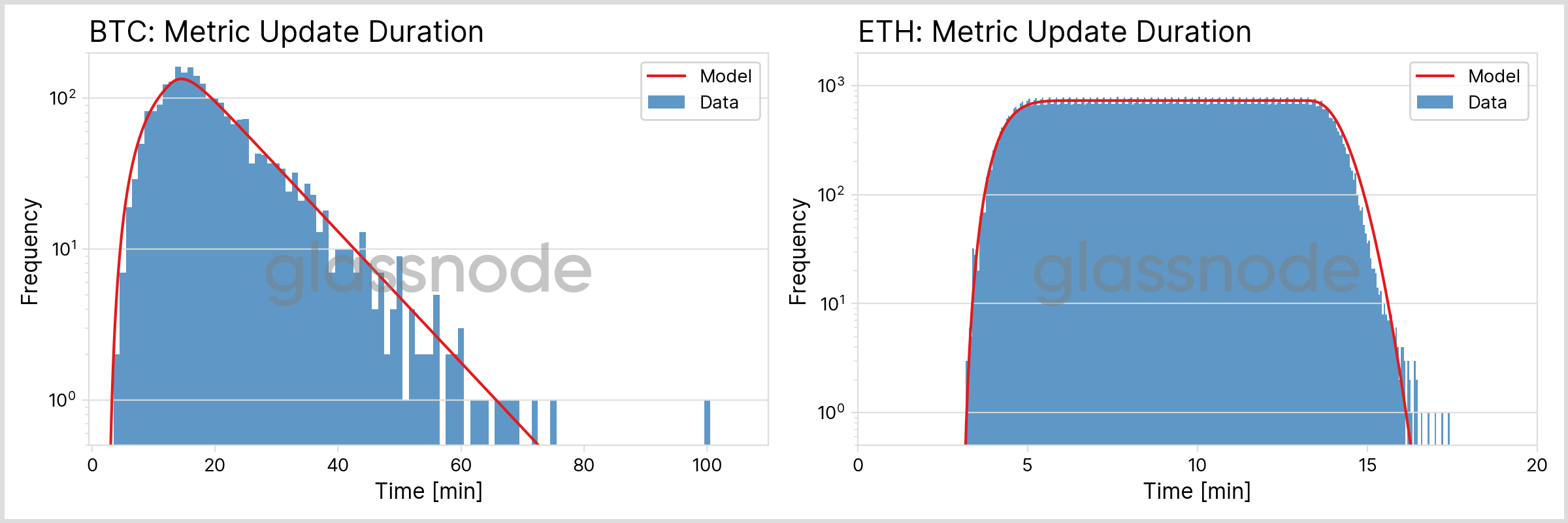
Not surprisingly, due to the lower block interval and the reduced confirmation period, we can observe that new data enters our ETH metrics quicker than for BTC. While we can expect that an ETH block has entered our metrics after around 15 minutes, the long-tailed distribution for BTC causes the duration to be somewhere between 30 minutes and 1 hour, with the exact number determined by the chosen probability threshold.
The following table summarizes the key quantities for the found distributions (metrics with 10 min resolution).
| BTC | ETH (PoW) | ETH (PoS) | |
|---|---|---|---|
| mean | 20 min | 10 min | 9 min |
| 25th percentile | 13 min | 7 min | 7 min |
| median | 18 min | 10 min | 9 min |
| 75th percentile | 25 min | 12 min | 12 min |
| 90th percentile | 34 min | 14 min | 13 min |
| 99th percentile | 57 min | 16 min | 15 min |
When is a data point complete?
The discussion so far has been about individual blocks and when they enter our metrics. However, we can ask a complementary question: How long does it take until all blocks in an aggregation interval have been collected? Or stated differently: When have all blocks been processed that contribute to a common data point in a metric, rendering a data point complete?
The term “completeness” used here does not necessarily imply that a data point is immutable: Its value will not change anymore due to the inclusion of new blocks, but there may be other means by which the data point receives updates. We will discuss such causes in the section on “Data Mutability”.
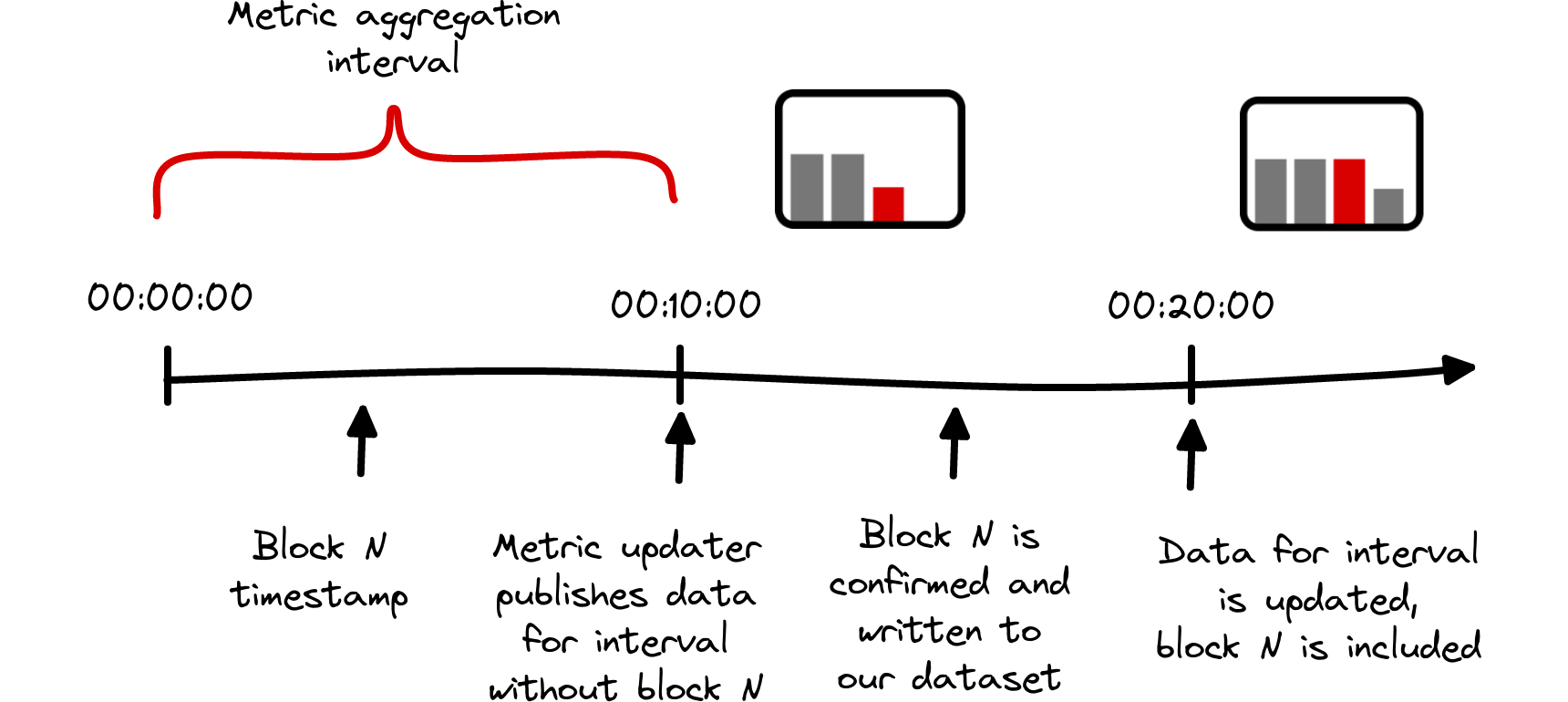
Repeated updates
From the discussion above it is already clear that in general not all blocks are immediately included once a new data point is released, this is due to the intrinsic delays a single block can encounter on its way into the metrics.
For example, let’s consider the case that is depicted in Fig. 6. Further, we assume an exaggerated timestamp 00:09:59 for block N, which eventually will contribute to the data point 00:00:00(Please note that our metric timestamps always refer to the beginning of the time interval in question). For our 10 minute resolution metrics, this data is first computed by our updaters that are triggered at 00:10:00, i.e. only one second after the block was created. Obviously, this interval is way too short to allow for propagation between the blockchain nodes, subsequent confirmation, data processing etc. Hence, it is more likely that the block’s data will be picked up at 00:20:00 only and retrospectively enter the data point, thereby modifying the existing value. This cause for data mutation is particularly relevant for blockchains with a high block frequency.
A similar situation can occur due to non-ordered BTC timestamps (see Fig. 3), as foreshadowed above: A new block, that is added to the blockchain and which has a timestamp that is smaller than the one from the previous block, can change an earlier data point. Fortunately, such negative intervals between blocks are bounded and rarely occurred within the last few years, as shown in Fig. 3.
Delayed releases
An interesting edge case of quite a different nature can occur for Bitcoin: Instead of having multiple blocks that enter the same data point in a metric, we can also encounter the case where no blocks lie in the aggregation interval. This can emerge for metrics with 10 minute and (more infrequently) 1 hour resolution, because the typical block interval is of the same order. In contrast, the ETH blockchain always contains at least a few blocks per data point even at 10 min resolution, which can be seen from the interval distribution in Fig. 2.
Such “empty” data points will be released together with the next “non-empty” data point, that again includes real blocks. Their value depend on the character of the metric: E.g. for Transaction Counts the value is filled with zero, while for Circulating Supply the last known value is forward-filled.
Quantifying completeness
To approach the question on data completeness which we raised in the beginning of this section, we consider two timescales with different starting points.
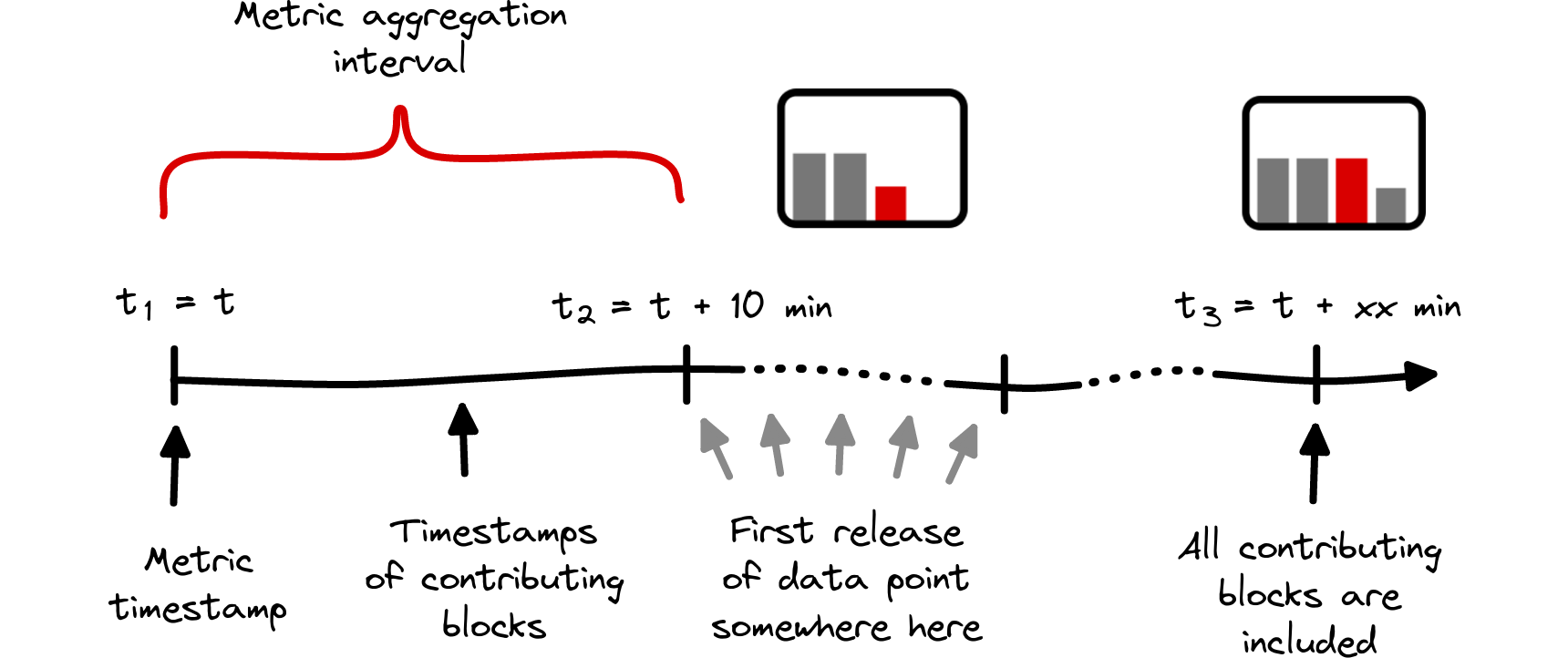
- The duration between a data point’s timestamp and the time when no further blocks contribute. In the sketch shown in Fig. 7, this corresponds to times t₁ until t₃.
- The duration between the first release of a data point and the time of data completeness, corresponding to the interval t₂ – t₃ in Fig. 7. Since the release of a new data point always follows the metric timestamp, this duration is shorter.
For clarity, we focus on metrics with 10 minute resolution again and further neglect the updater runtime, to arrive at a result independent of the chosen metric. From our data we can extract the numbers for typical BTC metrics as shown in Fig. 8 below.
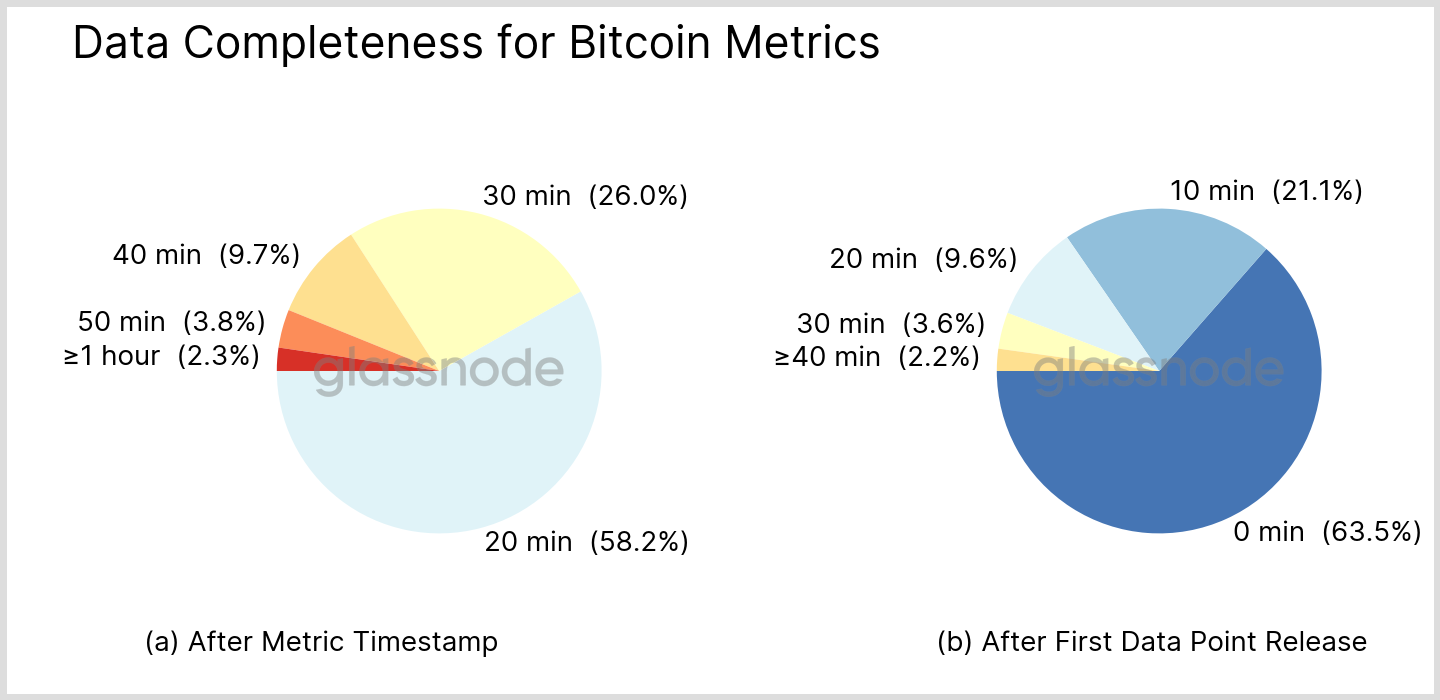
From the chart on the right in Fig. 8, we can see that for about 2/3 of newly released data points the values are already final and won’t change anymore due to additional blocks. Repeated updates for the rest of the data points become more and more infrequent. When taking the metric timestamp as reference (left panel in Fig. 8), about 85% of the data points are complete within half an hour.
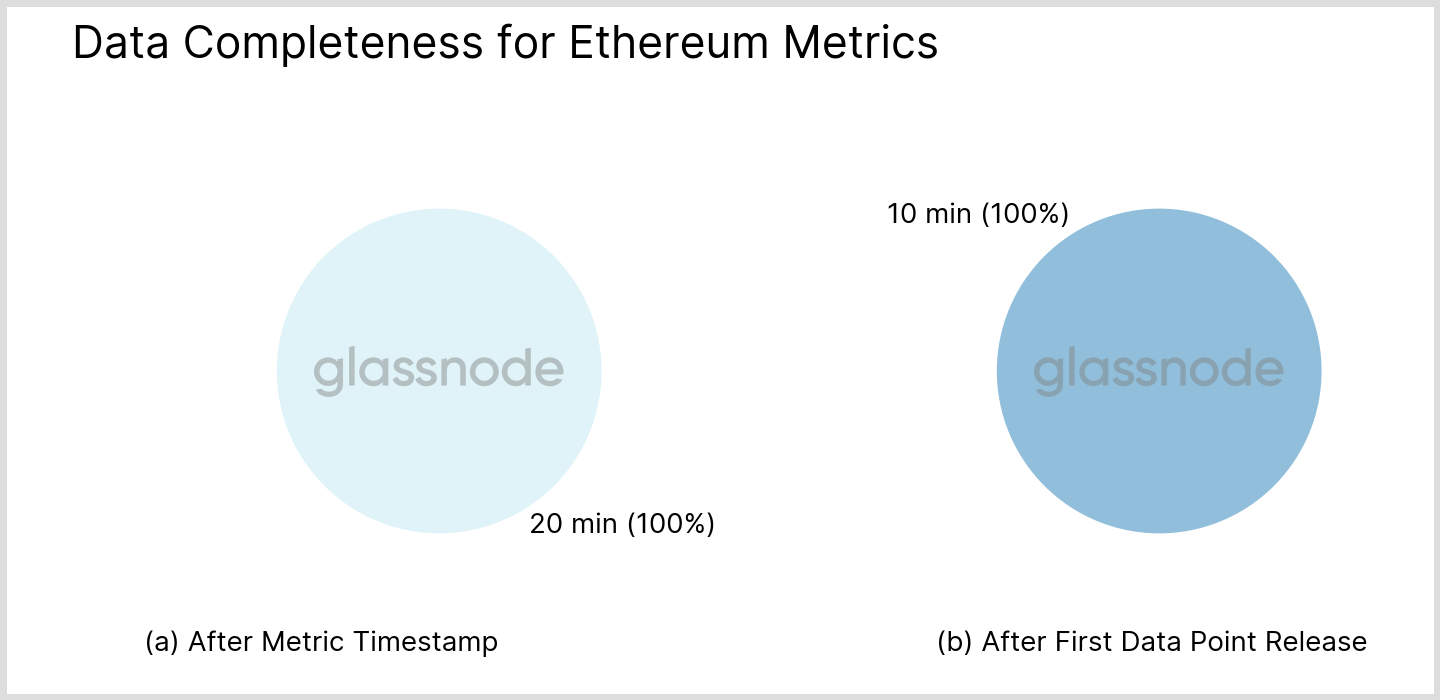
For ETH (both PoW and PoS), the results are less spectacular, see Fig. 9 below. The mean block interval (~12 sec) is much lower than the considered metric resolution (10 min) and therefore the first possibility for data mutation which was illustrated in section “Repeated updates” affects all data points. For the same reason, any tails in the temporal distribution are absent.
Data Mutability
In the scope of changing data points, we considered causes intrinsic to all our on-chain metrics so far. For the reasons discussed, somehow paradoxically, even the most fundamental metrics derived from the bare blockchain are subject to change, even if the underlying blockchain is immutable. As we have seen, the cause of this is the inevitable delay when we process new blocks. Fortunately, the effect of changing data applies only to the most recent timestamps and, as discussed above, all values stabilize within a short time frame.
But beside this effect there may be other causes for changing data, with their appearance related to the type of a metric. It is therefore instructive to dissect these types in ascending order of complexity.
Causes for changing data
Standard on-chain metrics
We denote metrics that are solely derived from the bare blockchain data as “standard metrics”. Additional information, e.g. data from external sources or advanced statistical analyses, does not enter their computation. Examples encompass the Number of Blocks or the Supply held by Whale Addresses. The following mechanisms for altering data can apply:
- Intrinsic delays: Like we discussed above in detail, the last few data points in a metric are subject to change due to the unavoidable delay within the “blocks’ journey into our metrics”.
- Chain reorganization (“reorg”): The longest blockchain is the globally accepted one. If however two chains have equal size, it may happen that a node temporarily follows the “incorrect” blockchain. In such cases it can be necessary to discard several blocks and sync with the main chain again. In turn, metrics derived from the discard branch must be updated. To minimize this effect, we therefore wait a certain number of confirming blocks, to verify the state of our nodes’ branches (see the related discussion in the part on metric availability above). Thanks to this precautionary measure we hardly observe any data changes caused by reorgs in practice.
Metrics including external data
Several of our metrics require additional third-party data from external sources. The most prominent example for this is the current and historic price for an asset. Examples for such metrics is the Market Capitalization or Share of Addresses in Profit. In addition to the data changes from above, we may encounter the following one:
- Delayed, incorrect, or absent data from third-party data providers: Such events are rare, but may require a recomputation of the affected metrics starting from the point in time where the extra data had to be updated or replaced. Such changes are always announced in our Changelog.
Clustering metrics
In case of Bitcoin we continuously run multiple heuristics in a highly automated fashion, that detect sets of addresses, which are with very high accuracy controlled by a single entity each. This creates clusters of addresses, some of which can be attributed to a known entity (see here for more information). Many of our metrics make use of this extra “clustering layer”. Examples can be found in our vast set of “entity-adjusted metrics” (see our docs for a list). On top of the already mentioned causes, we also encounter the following situation here:
- Address Clustering: As new addresses of a cluster are detected, the newly acquired clustering data makes it necessary to refresh the full historic data of a metric, for it to reflect the best possible knowledge we have on the blockchain. This is in contrast to the issues discussed so far, where the affected timestamps covered only a short span. Since address clustering is an automated process and can give rise to continuous changes in our data, we will devote a larger section to this topic below and discuss its impact in more detail.
Metrics devoted to individual entities and entity categories
Metrics of this type encompass Exchange Metrics, Miner Metrics, or the WBTC Supply at Custodians – in short: metrics that describe a particular named entity or a collection of those. To compute such metrics, we require sets of addresses, for which the owners are known. We periodically update our set of labels by various techniques and in case of BTC this process is supported by the aforementioned clustering data. Next to the causes for changing data that were already discussed above, the following effects can apply:
- Entity Whitelisting: When we deem the data quality for a new exchange or miner high enough, we enable support for this entity. This does not strictly mutate metrics, but views with the
aggregatedoption as filter will look different (e.g. when requesting the total balance of all exchanges). Changes to the list of supported exchanges or miners are announced in the Changelog. - Manual addition of new labels: As we add newly acquired labels, we face the same challenge as touched on in the explanation of changes due to new clustering data: Metrics may sometimes require a recomputation of their full historic data. Again, switching to a new set of labels is always announced in the Changelog.
Further causes for changing data
- Bugs and Outages: We are only humans and while errors should not happen, they can. In rare cases we have to revise or fix a metric, or experience issues with our software infrastructure. Such changes are always announced in our Changelog.
- Improved methodology: In rare instances we revise the way how a metric is computed. This can happen when we assume that the improved version is more beneficial to our users or when its approach is more comparable to those of other metrics, therefore enabling a higher degree of comparability. Again, such improvements are communicated in our Changelog.
The crux with “address clustering”
In our enumeration of possible causes for changing data we did encounter one particularly interesting case: “Address clustering” regularly requires full historic recomputations and, in contrast to the sporadic announcements in the Changelog, constitutes a constant and ubiquitous process. In this section we will dive into the details of “address clustering”.
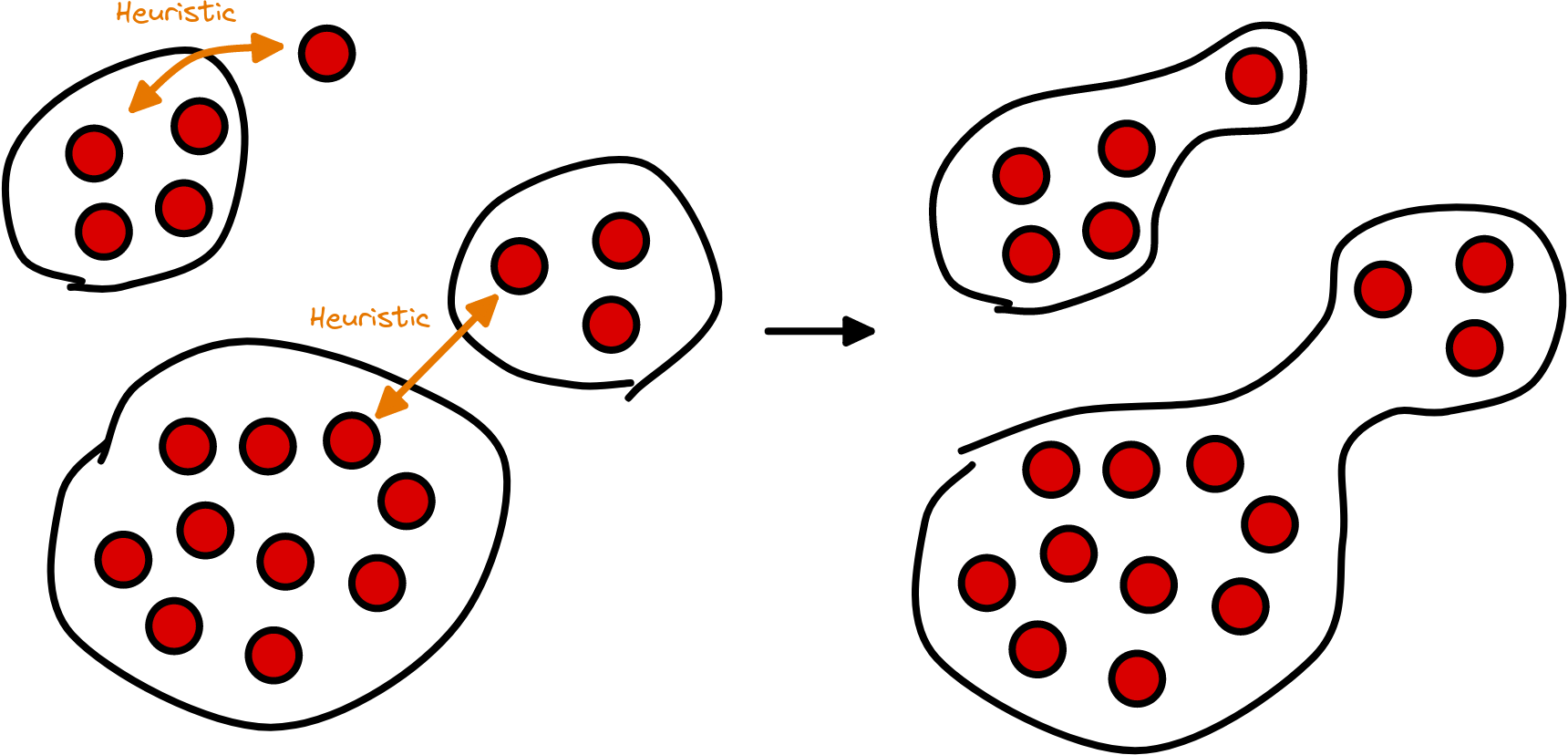
Our heuristics and clustering algorithms continuously group addresses together, that are controlled by a single entity. Based on this data, we can, e.g., omit any kind of change volume and infer the actual transfers on the blockchain. As time progresses, our heuristics detect more and more of such connections between addresses, therefore improving the quality of the address clusters (see Fig. 11 for an example).
Our philosophy at Glassnode regarding the address cluster is to use a conservative approach that reduces the number of false positive links between addresses. In view of newly created addresses on the blockchain this means that very often these addresses are not immediately added to existing clusters, this happens only as time progresses and more data on the addresses is collected.
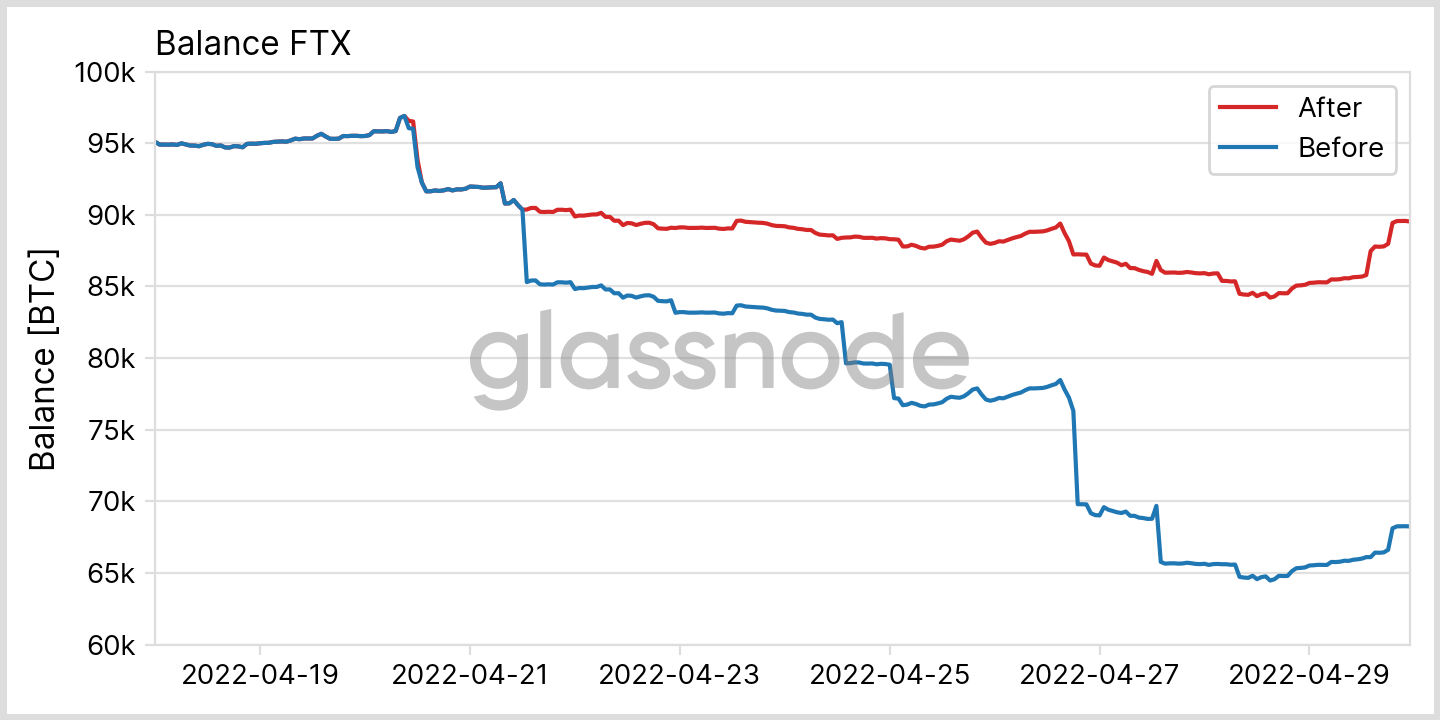
This has some interesting consequences: Coming back to the example from above, a transaction that was previously recognized as a transfer between two different parties may suddenly become an internal transfer only, thereby altering the contribution to all dependent metrics. We have elaborated on this problem in the context of exchange metrics in a previous article.
In order for our metrics to reflect the latest state of the clustering data, and therefore providing the best view on the blockchain, it is required to constantly update historic data of a metric as well. In practice this is achieved in two ways (also see Fig. 12 for illustration):
- Full daily recomputations: All metrics that employ clustering data are fully recomputed once a day. Currently our pipelines for this are started at 00:30 UTC and depending on the complexity and extent of a metric, the updated metric is released between 01:10 and 02:40 UTC. This includes all available resolutions per metric.
- Rolling updates: In case of our metrics with 1h or 10min resolution we recompute the values for the last 6 hours in each update to the metric. For example, if our updater runs at 10:00:00, it will not only append a new data point to the metric, but apply the full clustering knowledge to all timestamps between 04:00:00 and 10:00:00. This ensures that new clustering data enters the metrics as fast as possible, without having to wait for the daily full historic update.
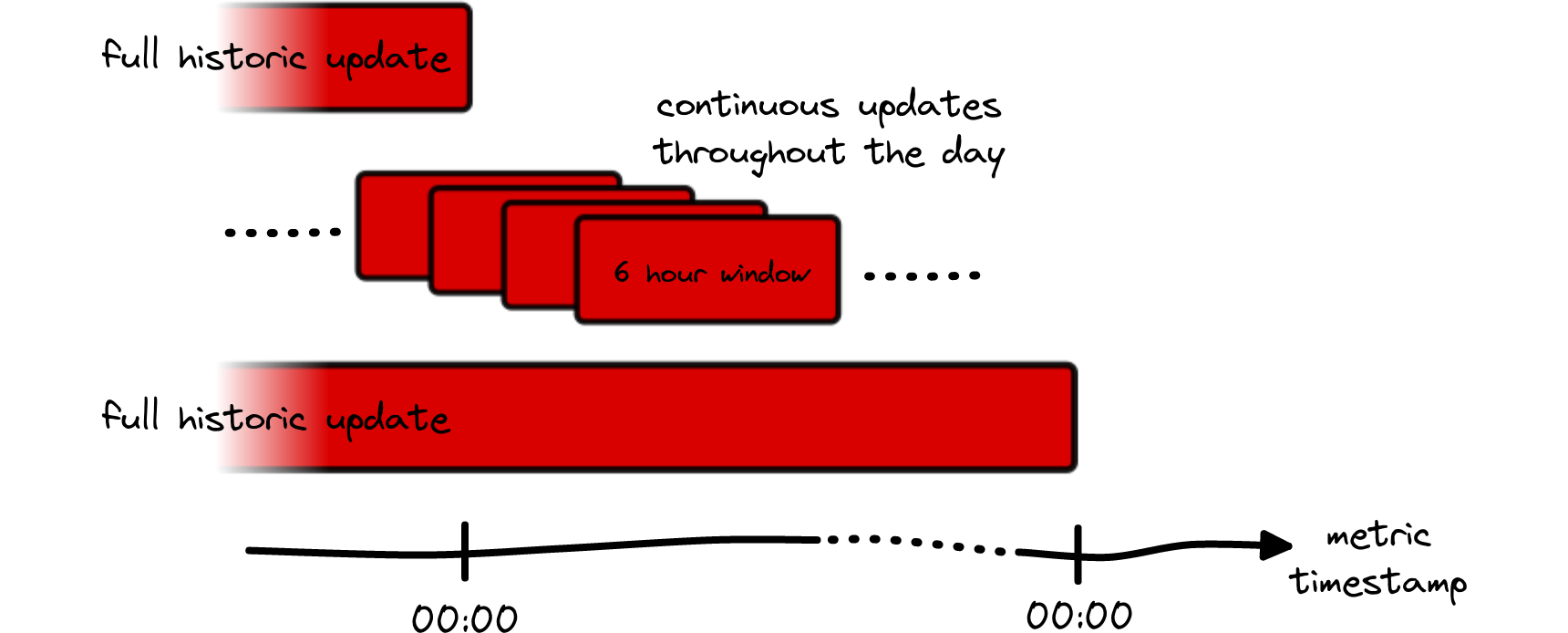
The natural question to ask here is: How long does it take until the values for a metric converge? When have we collected enough clustering data to render a value stable?
Clustering convergence
The impact of new clustering data on the different metrics can be very different, but according to our past observations we can typically distinguish two broad classes:
- Activity-based clustering metrics are directly inferred from the transactions on the blockchain in the time aggregation interval of interest. Examples for this are the Number of Transfers, the Exchange Inflow Volume, or the Average Lifespan of Spent Coins.
- State-based clustering metrics on the other hand represent current snapshots of the blockchain. Transactions in the time aggregation interval can modify this state, but do not define it per se. As a rule of thumb: To compute such a metric not only the current time interval, but all previous times have to be considered. Examples are the Number of Whales, the amount of Liquid Supply, or the Long-Term Holder Position Change.
Our clustering-related metrics for which we provide 1h and 10min resolution belong to the former set (with the exception of Exchange Balances, which, however, can be indirectly inferred from the exchanges’ activity and thus can be regarded as activity-based metrics in the following). As explained above, we use a rolling window with a length of six hours to update the last few values for these metrics. Comparing the hereby derived time series, we can quantify the typical changes and estimate a convergence timescale.
Ideally we would like to quantify the convergence with a unified method across all metrics, yielding a single number only for each metric. However, since metrics have very different characteristics and their values are differently distributed, this appears infeasible. For instance, taking the relative difference of the initial and the converged values will give rise to large deviations when the metric is allowed to fluctuate around zero. Similar, using absolute differences may lead to wrong conclusions for metrics that exhibit a significant constant offset. Therefore we rather take a more visual approach below.
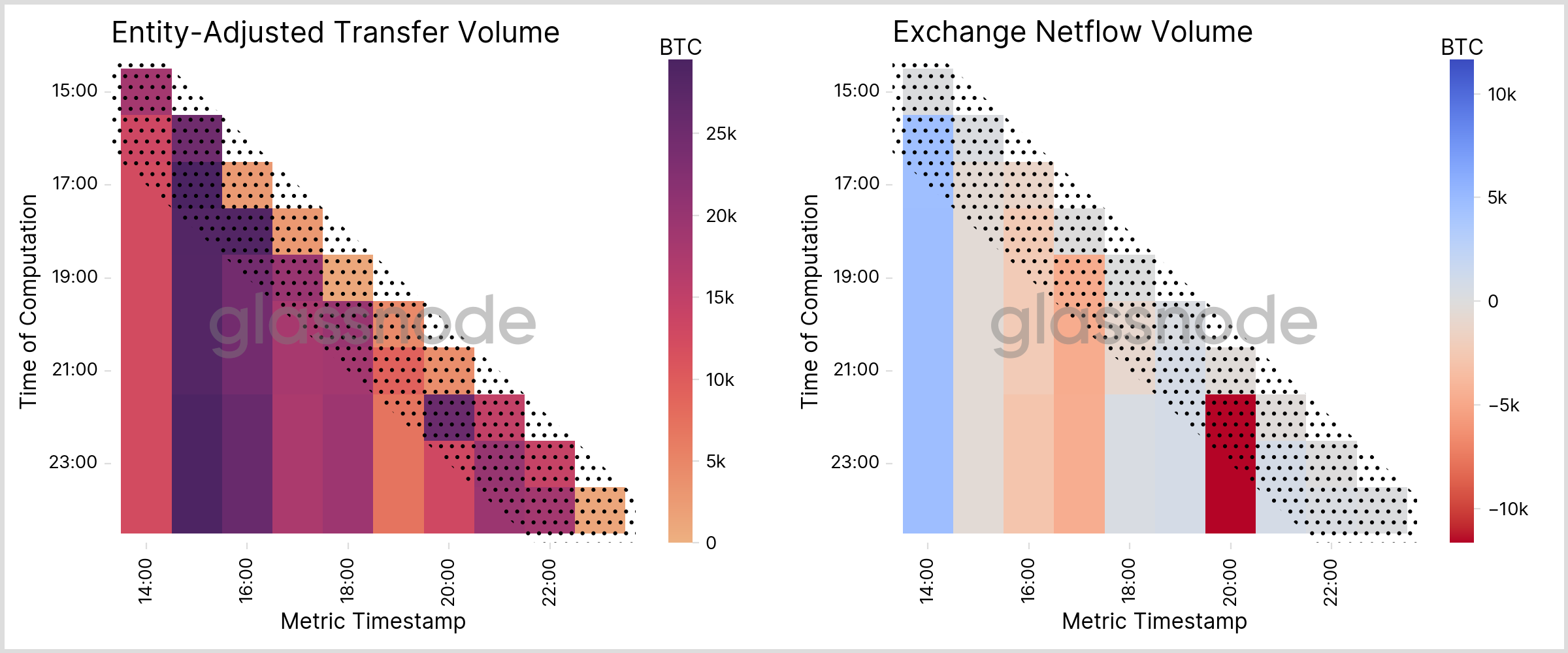
In Fig. 13 we present two exemplary metrics with 1h resolution that utilize clustering data and show how the metric values change with each computation iteration. It is apparent that the data often fluctuates within the first two hours after the initial release, as indicated in the dotted sections. After this, though, we observe that values remain rather constant (vertical “bars”) and additional clustering knowledge is of small effect only. We can therefore conclude that activity-based clustering metrics typically converge in ~2 hours.
The reason for this can be understood by the following argument: Activity-based metrics are dominated by contributions from entities with a high activity. At the same time, a high activity allows us to collect more statistical information on the involved addresses and to apply our heuristics more often, which in turn quickly leads to comprehensive clustering data for the high-activity entities. As such, the metrics swiftly converge.
Unfortunately, fast convergence is not guaranteed for metrics where highly active entities do not dominate the signal and for several state-based metrics, as we will see below.
Convergence of Illiquid Supply – A case study
To illustrate the problem of metric convergence we chose the metric Illiquid Supply as an example. It is computed by summing up the balances of all entities that are below a certain liquidity threshold. For more details on the metric and its interpretation see our previous article here. In terms of address clustering we face the following problem: Let’s assume we detect a new address on the blockchain, which does not spend any of its coins for a long time. Therefore, our heuristics can often not assign the address to an existing cluster – a cluster which may actually be highly liquid – and therefore oppose the metric’s meaning. Until coins are moved, the address’ balance will contribute to the illiquid supply and hence we overestimate the value for the metric.
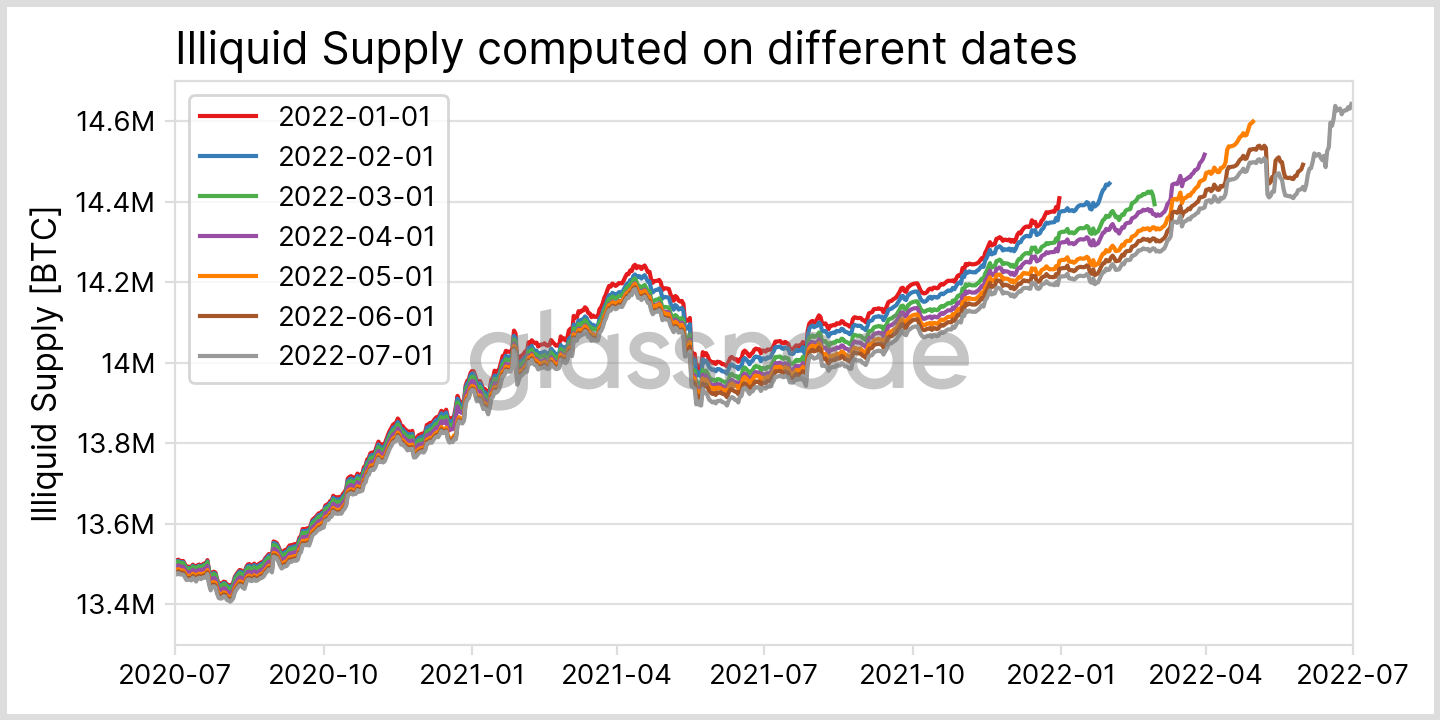
To quantify this effect we can, for example, again compare the data computed at different times, see Fig. 14. While the relative changes between consecutive runs are negligible, they sum up over time. Comparing the first and the last computation from Fig. 14 directly, we find that the values for the last ~30 days in the metric are still subject to change by more than one percent. A similar analysis was performed by Willi Woo, who concluded that most changes occur in the first 3 months and full convergence takes 4 years. Despite this long timescale, day-to-day changes in the metric and general drifts are stable already very early on – only the absolute numbers have not converged yet.
What to do in case of changing metrics?
We have addressed several factors that can cause data mutations in our metrics. In the following, we want to present a few recommended ways how to deal with such changes from a user perspective.
Our aspiration is to provide the best possible and most comprehensive data in the metrics, which is the reason why we strive for metric updates in the first place. But as we have seen above, historic data is typically of higher stability, while the more recent data points are subject to change more often.
If one is interested in a metric from a qualitative point of view, we generally advise to not draw any strong conclusions from the most recent two hours, as these timestamps may still highly fluctuate. Indeed, for many such entity-adjusted metrics, daily resolution is the highest we provide to account for this, where appropriate. Further, if the metric of interest does not depict an activity dominated by a certain class of entities, absolute numbers should be taken with a grain of salt. Long term trends and day-to-day fluctuations, however, are generally stable.
The situation is different if the metrics are used for quantitative purposes, such as applications in machine learning or trading. Due to the repeated historic updates to our metrics that utilize clustering data, one has to expect information leakage from future clustering knowledge into data of old timestamps. This introduces a look-ahead bias, which was denoted as one of the “Seven sins of quantitative investing” by Y. Luo et al. Citing from their work, “we should use point-in-time data for all backtesting purposes”.
Immutable data: Enter point-in-time metrics
Point-in-time (PIT) data refers to snapshots taken at a particular moment in time, without any future revisions to the data. In the context of metrics, this means data points are frozen at the very moment they are released and never modified afterwards – no matter for including additional blocks or improving the clustering knowledge. This different update approach is visualized below in Fig. 15.
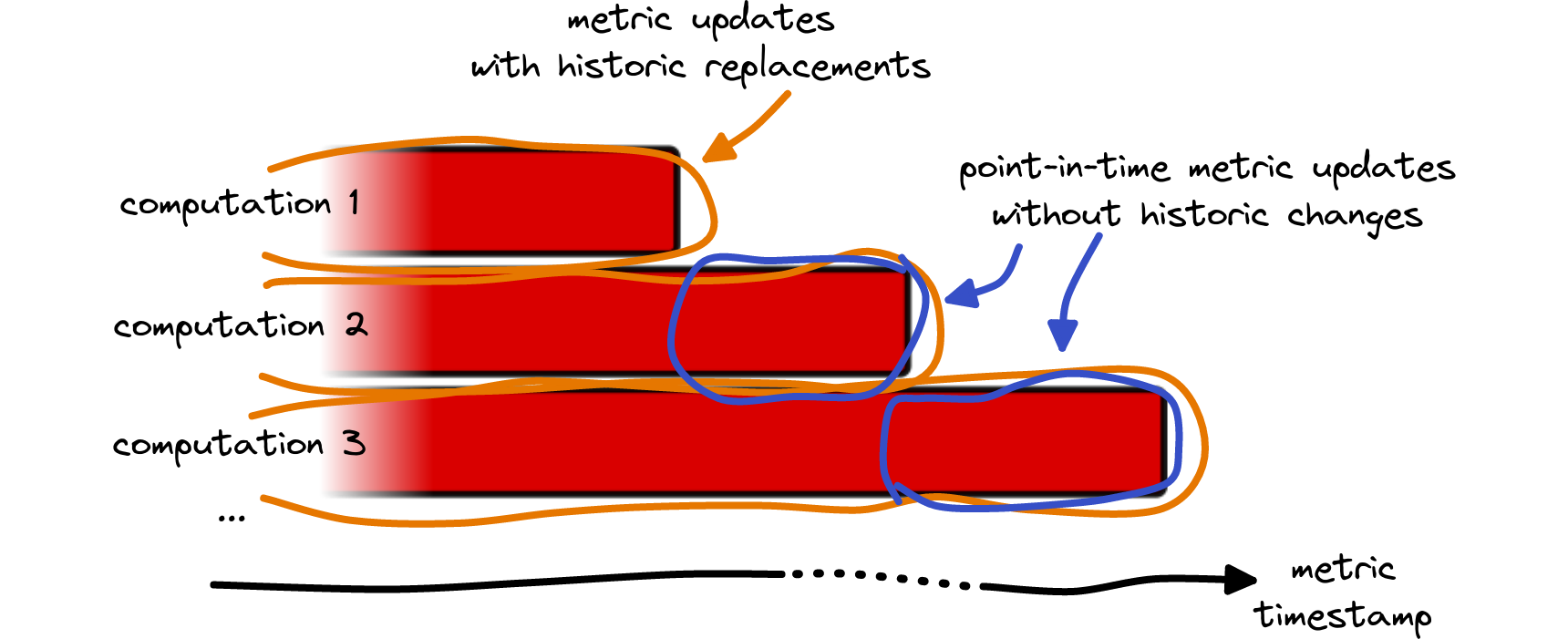
Creating such metrics with an immutable history has always been possible by periodically fetching data from our API and keeping every new data point only. However, this required some manual engineering overhead for all users separately and allegedly caused problems with rate limits. That’s why we are happy that we can extend our API offering with a large set of “Point-in-time metrics” as of today.
Our new PIT metrics provide immutable data in the sense that they are strictly append-only. Naturally, they don’t necessarily represent the best knowledge we have on the blockchain – this demand is met with our existing (mutable) metrics as always. A comparison of our existing metrics with the new point-in-time set can be seen in Fig. 16.
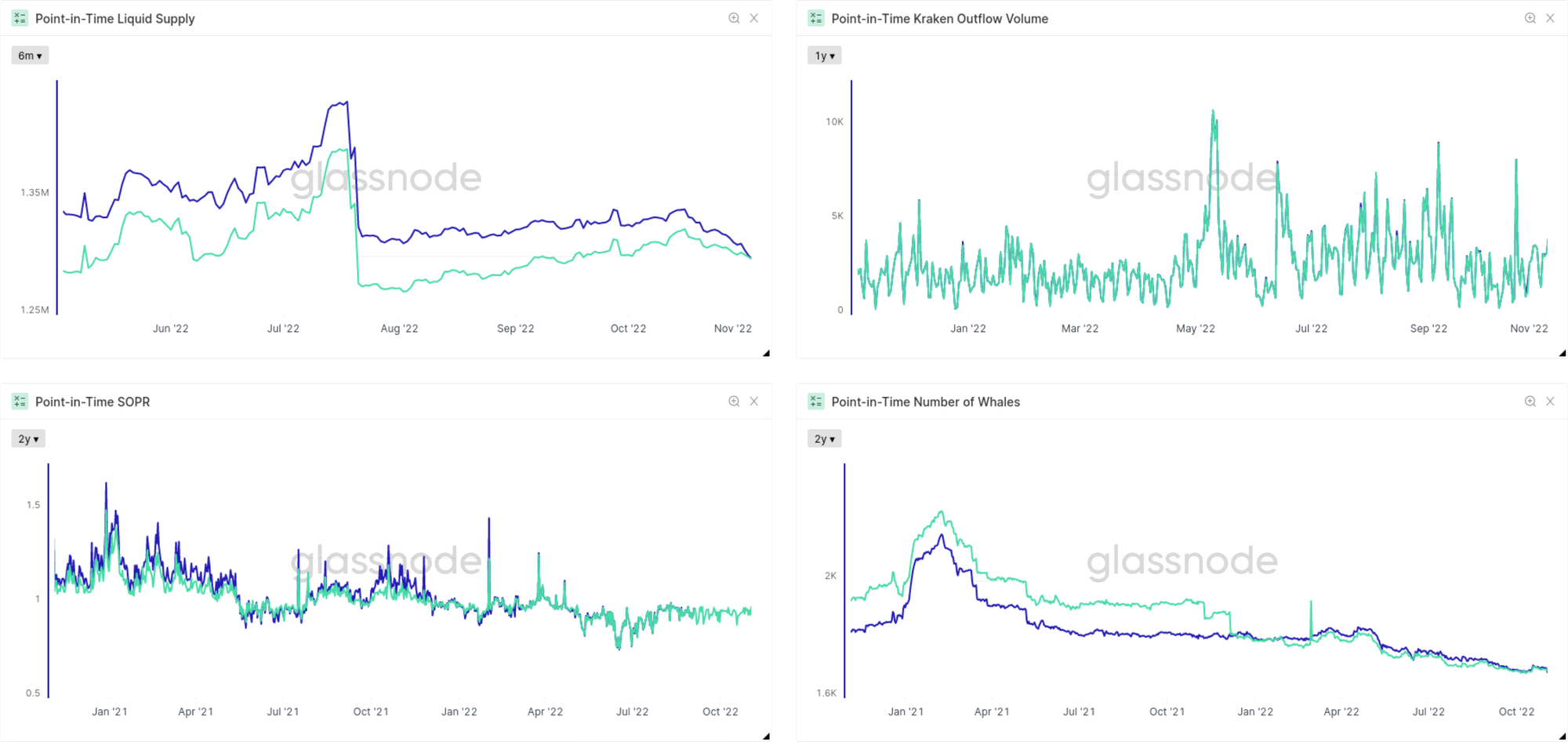
In the section on Data Mutability we found that “state-based metrics” are more susceptible to changes in the historic data than metrics that instead show “activity”. The same holds true for the comparison of mutable and point-in-time metrics: Activity-based metrics exhibit a larger overlap (on the scale of the typical metric variance), while state-based metrics often show larger discrepancies over time.
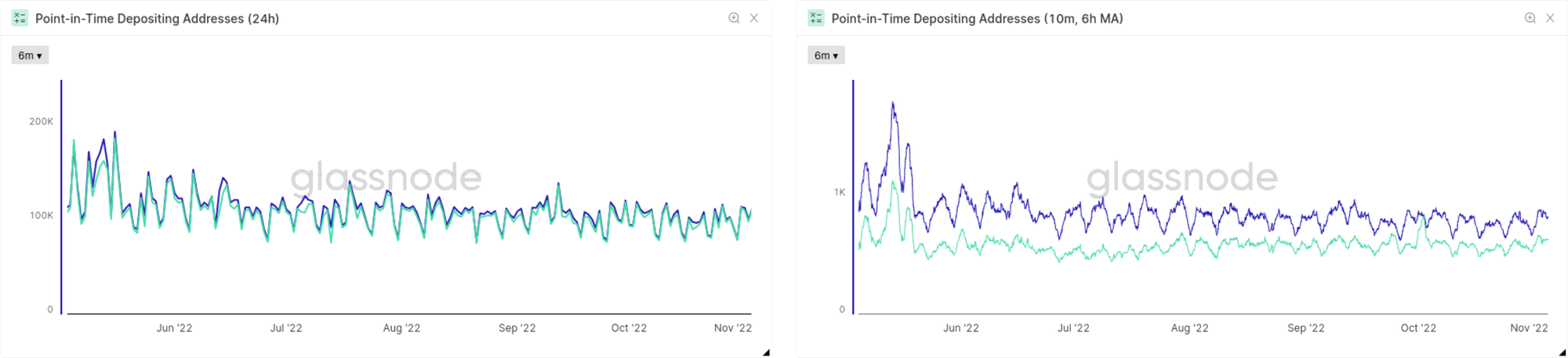
Another interesting insight we can directly gain from the point-in-time metrics is their behavior for different resolutions. In Fig. 17 we present the Number of Addresses Depositing to Exchanges as an example. In all cases the point-in-time version underestimates the data that was derived with later clustering and label knowledge, but the discrepancy is much stronger pronounced when considering the metric with 10 minute resolution. This can be well understood, though: When the very first value is computed for the data with 24h resolution, the majority of contributing blocks already have an age well above 2 hours, which is the time scale which we derived earlier to quantify convergence for activity-based metrics. Consequently, the overall value derived for the point-in-time metrics is close to convergence as well. In contrast, for higher resolutions hardly any of the contributing blocks have the required maturity level when the metric value is frozen into the point-in-time metric version.
Summary
We discussed different factors that influence when a metric receives updates and derived distributions for the expected delays. Further, we looked at different factors that make it necessary to update metric values beyond the latest few timestamps only. In particular, we have seen that address clustering and manual addition of labels entail full historic recomputation of a metric. Such historic updates make sure that the data shows the maximum available knowledge we have on the blockchain, but can cause a strong look-ahead bias. To avoid said problem, we introduced point-in-time metrics for which all historic data is immutable, rendering them an ideal candidate for applications in model backtesting and related fields.


Disclaimer: This report does not provide any investment advice. All data is provided for information and educational purposes only. No investment decision shall be based on the information provided here and you are solely responsible for your own investment decisions.
- Join our Telegram channel
- Visit Glassnode Forum for long-form discussions and analysis.
- For on-chain metrics, dashboards, and alerts, visit Glassnode Studio
- For automated alerts on core on-chain metrics and activity on exchanges, visit our Glassnode Alerts Twitter
